Augmented Analytics: Entdecken Sie die Prognoseszenarien mit Smart Predict und ihre Funktionsweise

Im ersten Artikel dieser Serie haben wir uns einen Überblick verschafft, welche KI-Funktionen in der SAP Analytics Cloud (SAC) angeboten werden und ein tiefer Einblick in den Chatbot „Just Ask“ hat spannende Fakten aufgedeckt. Jetzt ist der richtige Moment, sich anzuschnallen, denn es wird ein wenig technischer!

In diesem Beitrag werden wir uns auf folgende Prognoseszenarien mit Smart Predict fokussieren: Zeitreihenprognose (Time Series Forecast), Regression und Klassifikation (Classification). Alle in diesem Beitrag dargestellten Prognoseszenarien stehen im Kontext von Augmented Analytics und der SAP Analytics Cloud (SAC).

Prognoseszenarien mit Smart Predict

Den zweiten großen KI-Funktionsbereich in der SAC bilden die Smart Predict- oder Prognoseszenarien. Der Name macht bereits deutlich, dass es sich dabei um Algorithmen für Maschinelles Lernen (ML) handelt, die Sie bei der Vorhersage der Ergebnisse bestimmter betrieblicher Fragestellungen unterstützen.

In der SAC gibt es drei Typen von Prognoseszenarien:

1. Klassifikation (Classification)
2. Regression (Regression)
3. Zeitreihenprognose (Time Series Forecast)

Dabei muss der Anwender den Typ des Prognoseszenarios auswählen, der am besten zu seiner Fragestellung passt.

Allen drei oben genannten Machine-Learning-Szenarien haben gemeinsam, dass man das System zuerst mit sogenannten (historischen) Ist-Trainingsdaten füttern muss. Diese Daten werden durch die Prognosealgorithmen hinsichtlich der inhärenten Zusammenhänge analysiert und es wird ein konkretes Prognosemodell erstellt, das zum einen die Vergangenheitswerte in der vorliegenden Form erklärt und gleichzeitig verlässlich (robust) hinsichtlich der zu prognostizierenden Werte ist.

Um das optimale Modell zu finden, nutzt das System Validierungslogiken und mathematisch, statistische Kennziffern zur Beurteilung der Prognosegüte des Models. Diese Metriken sind der Root Mean Squared Error (RMSE) für die Regression, die Accuracy (Anzahl der korrekten Vorhersagen/Gesamtzahl der Vorhersagen) und Total Loss für die Klassifikation und der Mean Absolute Percentage Error (MAPE) für die Zeitreihenprognose.

Im Fall eines Zeitreihen Forecasts bedeutet ein MAPE von 5 %, dass die durchschnittliche Differenz zwischen dem prognostizierten Wert und dem tatsächlichen Wert 5 % beträgt. In jedem Prognoseszenario können sie mehrere Prognosemodelle erstellen und diese mit verschiedenen Parametrisierungen vom System berechnen lassen.

Der gemeinsame Grundgedanke hinter diesen Konzepten ist die Verwendung von Algorithmen und statistischen Modellen, um Muster in Daten zu erkennen und diese Muster zu nutzen, um nützliche Vorhersagen zu treffen. Diese Vorhersagen können Unternehmen dabei helfen, bessere Entscheidungen zu treffen und ihre Prozesse zu optimieren. In der SAC können diese Modelle einfach erstellt und angewendet werden, was die Benutzerfreundlichkeit und Zugänglichkeit dieser fortschrittlichen Analysetools erhöhen.

Jeden der drei Typen wollen wir hinsichtlich Grundkonzept, Use Cases und Umsetzung in der SAC umreißen. Eine detaillierte Aufschlüsselung der hinter den Prognoseszenarien stehenden technischen Funktion und mathematischen Logiken würde den Rahmen diese Blogs sprengen und ist meiner Meinung nach an dieser Stelle auch nicht notwendig. Schließlich geht es bei der Nutzung von KI im Berufsalltag vor allem darum, dass die KI bzw. der Algorithmus im Hintergrund arbeitet und uns, ohne dass wir uns mit den hochkomplexen Details beschäftigen müssen, ein verlässliches Ergebnis mit einem nachweisbaren Mehrwert liefert. Natürlich soll nicht unerwähnt bleiben, dass es in der BTP (Business Technologie Platform) die sogenannte AI Foundation gibt, die als zentraler Ort für Entwickler fungiert, um dort Erweiterungen und Anwendungen zu erstellen die KI und generative KI einsetzen.

Szenario 1: Zeitreihenprognose (Time Series Forecast)

Die Zeitreihenprognose (Time Series Forecast) befasst sich mit der Vorhersage zukünftiger Werte einer Messgröße (Kennzahl), auf Grundlage ihrer Vergangenheitswerte. Die Zielgröße (Signalvariable) hat also immer einen konkreten Zeitbezug.

Folgende Fragestellungen können dabei beispielsweise beantwortet werden:

Wie werden sich die Verkaufszahlen bzw. Umsätze in meinen Verkaufsstellen in den kommenden Monaten entwickeln? Mit welchem Cash-Flow kann ich im nächsten Quartal rechnen? Wie werden sich meine Bestände in den nächsten Wochen entwickeln?

Die Prognosefunktion analysiert dabei die historische Kurve, die durch die Zeitreihendaten gebildet wird und zerlegt diese Kurve in ihre elementaren Komponenten Trend, Zyklen, Einflussfaktoren und Fluktuation.

• Der Trend kann dabei als die allgemeine Ausrichtung, die langfristige Entwicklungstendenz der Messgröße verstanden werden.
• In den Zyklen spiegeln sich periodische und/oder saisonale Ereignisse wider.
• Die Komponente Einflussfaktoren muss nur berücksichtigt werden, wenn es im Vorhersagemodell bzw. im Datensatz weitere Variablen (Merkmale) gibt, die Einfluss auf das Prognoseergebnis nehmen.
• Die sogenannte Fluktuation ist das was übrig bleibt, wenn Trend, Zyklus und ggf. die gefundenen Einflussfaktoren vom Ergebnis abgezogen werden.

Neben dieser sogenannten additiven Technik kommt unter Umständen auch die Technik der sogenannten Exponentiellen Glättung (Einfache-, Doppelte- und Dreifache Exponentielle Glättung) zum Einsatz. Speziell dann, wenn es in der Zeitreihe „Störungen“ in den Amplituden der Zyklen und den Trendverläufen gibt, die die Ergebnisse der additiven Technik verzerren, sorgt die exponentielle Glättung für bessere Ergebnisse bei der Modellauswahl. Die Exponentiellen Glättung misst mittels eines Glättungsfaktors α aktuelleren Messwerten eine höhere Bedeutung zu als älteren Werten. Unterstützt werden die beiden Techniken durch das sogenannte Piecewise Trend Detection Verfahren durch das Brüche in den Trends und Zyklen erkannt werden können.

Parametrisierung der Zeitreihenprognose

Die Prognose kann auf Ebene beliebiger, im Datenmodell enthaltener Dimensionen erfolgen. Das System erzeugt dann einen Forecast für jede Kombination der gewählten Entity Dimensionen. Als Beispiel sei hier ein Vertriebsverantwortlicher genannt, für den es aufschlussreicher ist, die zukünftigen Umsätze pro Land und/oder Produktgruppe zu prognostizieren, anstatt in einer Summe über alle seine Produkte.

In den Settings des Models kann man unter „Influencers“, die im Datenmodell enthaltenen und oben erwähnten Einflussfaktoren hinterlegen, um die Genauigkeit der Vorhersage zu verbessern. Beispiele für solche Einflussfaktoren sind im Vertriebsumfeld beispielsweise ein auf einen bestimmten Zeitraum beschränkter Discount oder der Monatsultimo bzw. der erste Werktag eines Monats, an dem die Verkäufe besonders niedrig bzw. hoch sein können.

Um wunschgemäß hinreichend weit in die Zukunft prognostizieren zu können, müssen Sie dafür sorgen, dass ausreichend viele historische Werte vorhanden sind, die die Grundlage für die Prognose bilden. Es sollten historische Daten mit mindestens der fünffachen Länge des Prognosezeitraums im Trainings- und Validierungsdatenset enthalten sein.

Ein besonderer Mehrwert ist dadurch gegeben, dass die Ergebnisse des Zeitreihenprognose als Referenz- und/oder Planwert direkt in ein SAC-Planungsmodell übernommen werden können und so dem Planer neben den Istwerten als wertvolle Orientierungsgröße dienen.

Beispiel einer Zeitreihenprognose in der SAC

Anbei ein paar Impressionen eines Zeitreihen Forecast in der SAC. In dem Szenario soll prognostiziert werden, wie sich die Besucherzahlen in den Naturparks der USA zukünftig entwickeln. In den Screenshots finden Sie einige Erläuterungen, die wir Ihnen nachfolgend darstellen.

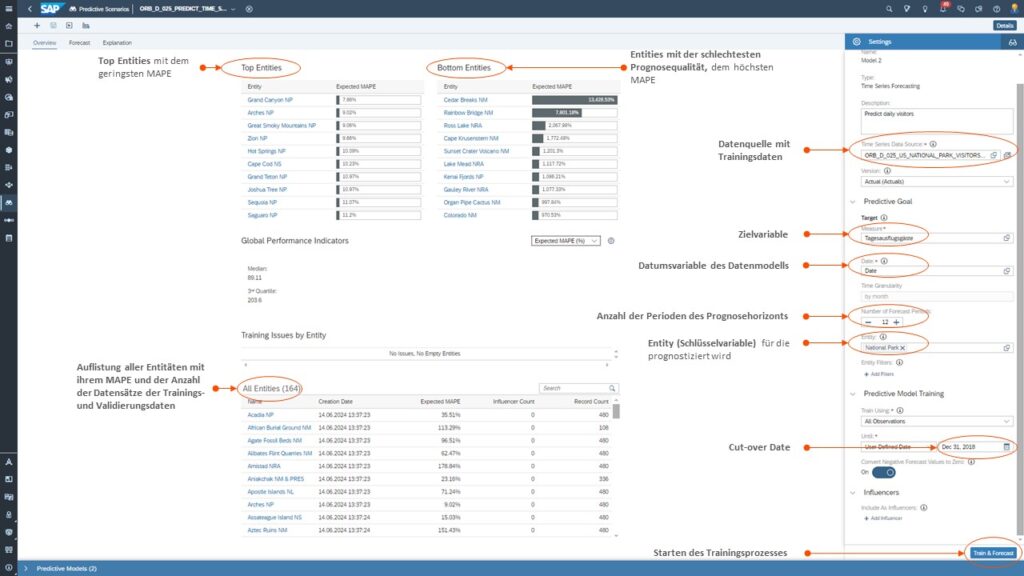
Tab 1: Zeitreihen Forecast – Überblick

Die nachfolgende Abbildung bietet Ihnen einen Gesamtüberblick auf das Prognoseergebnis und die der Prognose zu Grunde liegenden Settings.

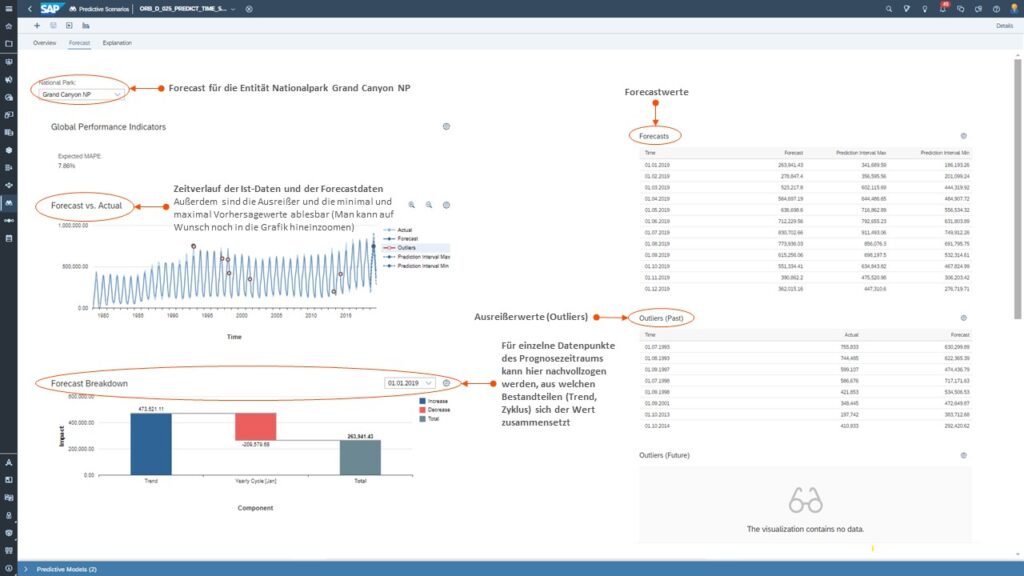
Tab 2: Forecast Ergebnisse

In der nächsten Abbildung können Sie sich die Ergebnisse für jede Entität detailliert anschauen.

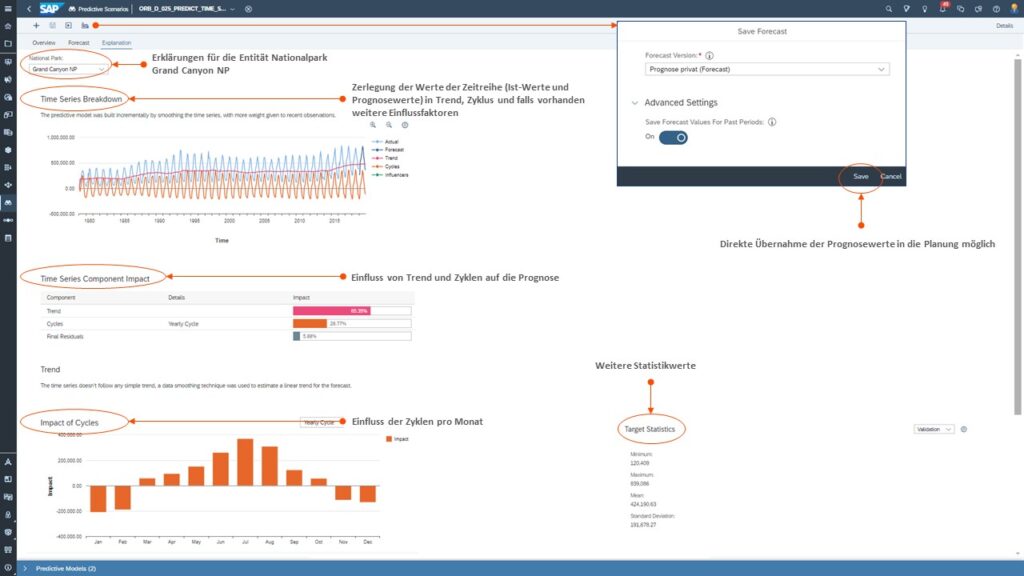
Tab 3: Forecast Erklärungen & dessen Weiterverwendung in der Planung

Im folgenden Schaubild sehen Sie, dass für jede Entität auf detaillierte Erklärungen zurückgegriffen werden kann. Außerdem können Sie erkennen, dass eine direkte Übernahme der Prognosewerte in die Planung möglich ist.

Szenario 2: Regression (Regression)

 Regression wird verwendet, um den Wert einer Messgröße, eine quantifizierbare Kennzahl, zu schätzen. Im Unterschied zum Zeitreihen Forecast ist bei der Regression der Zeitbezug nicht notwendig. Jede Zeile des Trainingsdatensatzes mit den historischen Daten repräsentiert eine Entität, die durch die Kombination einer Reihe von Dimensionen bzw. Variablen verkörpert wird. Das Ziel der Regression ist es, den Wert der Zielgröße für eine neue Entität, basierend auf den Werten der anderen Variablen vorherzusagen.

Folgende Fragestellungen können dabei beispielsweise beantwortet werden:

Mit welcher Verzögerung (Days Sales Outstanding) kann ich beim Zahlverhalten der einzelnen Kunden rechnen? Wie viele Produkte wird ein Kunde nächsten Monat/nächstes Quartal kaufen? Wie viel Geld gibt ein Kunde durchschnittlich in meinem Webshop aus?

Ein Kunde will z.B. wissen, mit welcher Anzahl von Kundenbeschwerden er in den folgenden Wochen rechnen muss. Die Grundlage für das Prognosemodell bilden dabei Datensätze die zum einen das Schlüsselmerkmal Woche, Einflussfaktoren (Candidate Influencers) wie z.B. die durchschnittliche Bearbeitungszeit der Beschwerden, die Anzahl der Kundenaufträgen, die Anzahl der Mitarbeiter im Kundenservice, Änderungen am Produkt in der jeweiligen Woche und als Zielvariable die Anzahl der Beschwerden enthält.

Lineare Regression

Um die theoretischen Grundlagen der Regressionsanalyse besser zu verstehen, betrachten wir zunächst die lineare Regression. Im klassischen Fall wird diese zur Schätzung des Werts einer Messgröße verwendet. Vereinfacht gesprochen hat sie folgenden Aufbau:

f(x)=c+y₁x₁+y₂x₂+…+y_nx_n

Dabei sind y₁, y₂, y₃,…,y_n die Koeffizienten (Gewichtungsfaktoren) für jeden der Prädikatoren (Einflussfaktoren) x₁, x₂,…,x_n des Models. c ist das sogenannte Intercept bzw. Bias, d.h. der Ergebniswert, der ermittelt wird, wenn alle unabhängigen Variablen gleich 0 sind. Über die Koeffizienten wird festgelegt, wie groß der Einfluss der Änderung einer Einheit einer einzelnen Candidate Influencer Variablen auf das Ergebnis ist, wenn alle anderen Variablen konstant gehalten werden. Beim Ergebnis handelt es sich, im Gegensatz zur im nächsten Abschnitt beleuchteten Klassifizierung, immer um numerische Werte.

In einem konkreten Beispiel könnte das System beispielsweise eine Regressionsfunktion zur Ermittlung des Preises eines Gebrauchtwagens ermitteln. x₁ bis x_n könnte beispielsweise durch Merkmale wie Fabrikat, Farbe des Autos, Alter des Autos, Checkheftgepflegt ja/nein, Klimaanlage vorhanden ja/nein, usw. stehen.

Eine idealisierte Regressionskurve könnte wie folgt aussehen:

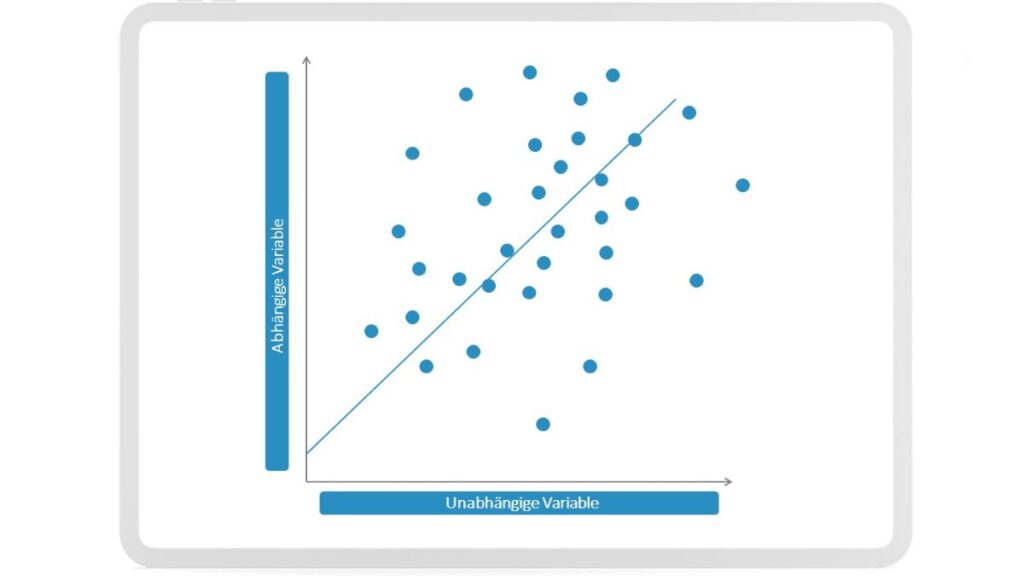
Over- und Underfitting

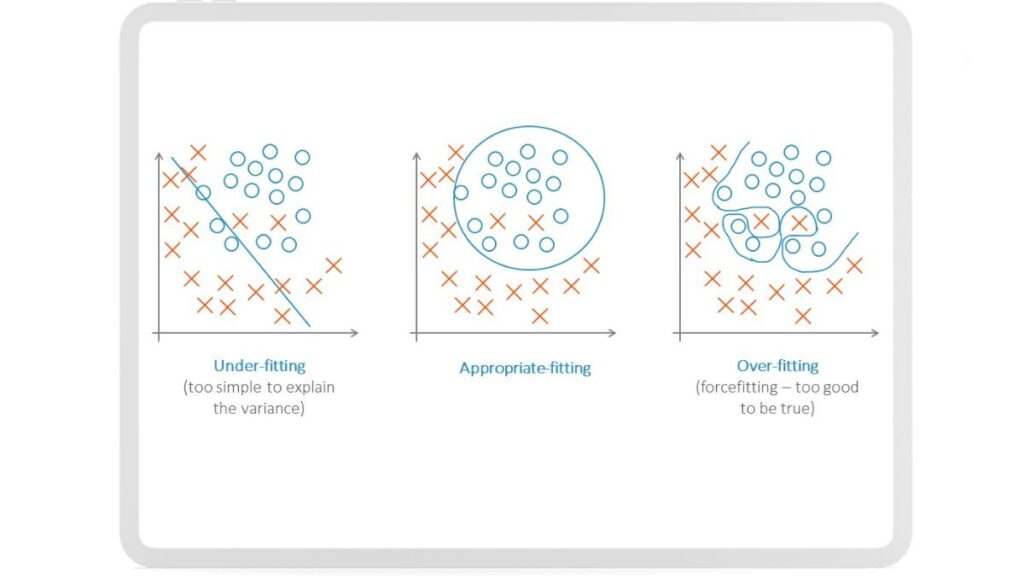
Mit welchen Techniken findet Smart Predict nun die Formel f(x)? Um dies zu verstehen, müssen wir uns erst mit dem Begriff Over- und Underfitting vertraut machen.

Overfitting tritt auf, wenn ein Modell die Trainingsdaten zu genau lernt und sich dabei auch auf zufällige Schwankungen einstellt, was zu schlechter Vorhersage bei neuen Daten führt.

Underfitting hingegen tritt auf, wenn das Modell zu einfach ist und die zugrundeliegenden Muster in den Daten nicht gut genug erfasst werden, was ebenfalls zu schlechten Vorhersagen führt.

Ein gutes Modell muss einen Mittelweg finden, um einerseits die Datenmuster präzise zu erfassen, andererseits aber auch so flexibel sein, um auf neue Daten richtig zu reagieren.

Entscheidungsbäume und Gradient Boosting Verfahren

Um die gesuchte Funktion zu ermitteln, nutzt das System das Konzept der sogenannten Entscheidungsbäume. Ein Entscheidungsbaum stellt Fragen zu den Einflussvariablen des Modells bzw. hinterfragt dessen Werte. Dabei beginnt das System mit einem leeren Baum und erzeugt immer mehr Verzweigungen bzw. Verästelungen. Der Datenbestand wird dadurch immer weiter geclustert. Am Ende eines Unterzweiges wird dann für die Zielvariable ein Wert ermittelt.

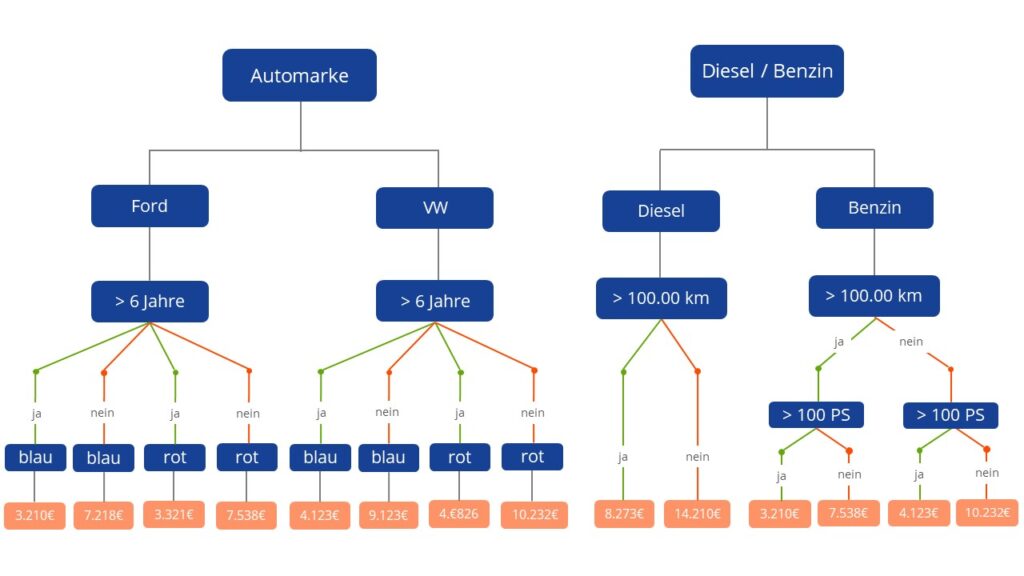
Das System ermittelt im Zuge des sogenannten Gradient Boosting Verfahrens eine Vielzahl an Entscheidungsbäumen. Mit Hilfe dieser Entscheidungsbäume werden entsprechende Muster in den Daten erschlossen und der Algorithmus tastet sich durch die Kombination der Ergebnisse der einzelnen Bäume an die realistischen Werte für die Ergebnisfunktion heran. Durch den Gradient Boosting Algorithmus wird eine Serie von kleinen, einfachen und schwachen Entscheidungsbäumen erstellt.

Der Sinn dahinter ist, dass eine Kombination aus mehreren einfachen Entscheidungsbäumen ein resilienteres Ergebnis liefert anstatt ein einzelner sehr tief verschachtelter Entscheidungsbaum. Dieser repräsentiert zwar im Ergebnis die Werte der Trainingsdaten u. U. perfekt, ist aber viel zu komplex und hinsichtlich der Prognosewerte zu ungenau. Dies würde somit zu einem Overfitting des Modells führen.

Die Formel f(x) wird iterativ verbessert, indem Residualfehler der vorherigen Bäume berücksichtigt und systematisch minimiert werden. Ein Residualfehler bezeichnet die Differenz zwischen einem beobachteten Wert und dem durch ein Modell vorhergesagten Wert. Durch diese Methode passt das System die Struktur der Entscheidungsbäume an, indem es die Daten durch rekursive Aufteilung in immer feinere Teilmengen segmentiert, bis eine hinreichend robuste Funktion für die Prognose gefunden wurde. Jeder Knoten im Baum repräsentiert eine Entscheidung basierend auf einem Merkmal, und die Blätter des Baums liefern die finalen Vorhersagen, die als Durchschnitt der Zielwerte in diesen Teilmengen berechnet werden. Vereinfacht gesagt, entspricht die Struktur der kleinen, iterativ gelernten Entscheidungsbäume den Koeffizienten in einem klassischen linearen Regressionsmodell.

Im Fall der Regression wird mit dem RMSE, dem Root Mean Square Error als Maß der Prognosegüte gearbeitet. Der RMSE ist die Quadratwurzel des durchschnittlichen Prognosefehlers. Je größer dieser ist, desto schlechter ist die Anpassung des Models an die tatsächlichen Werte.

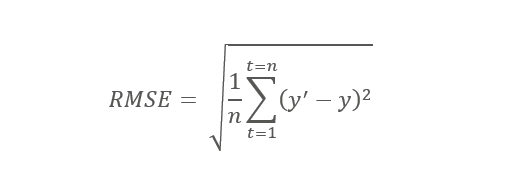
Dabei ist y‘ der prognostizierte Wert, y der Messwert, n die Gesamtzahl der Werte in der Trainingsmenge.

Beispiel eines Regressionsszenarios in der SAC

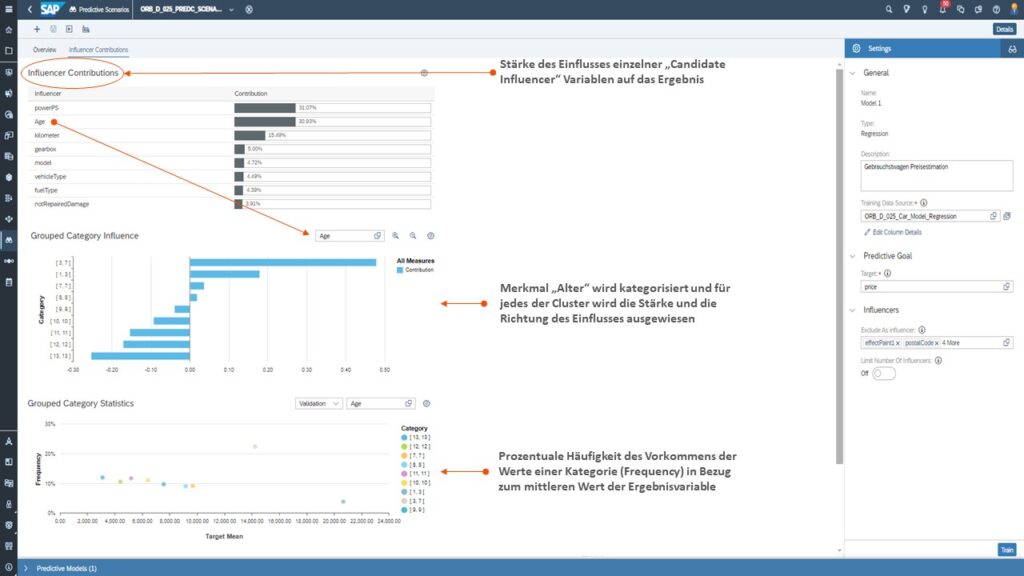
Anbei ein paar Impressionen eines Regressionsszenarios in der SAC. In dem Szenario soll der Preis für einen Gebrauchtwagen abhängig von bestimmten Einflussfaktoren wie beispielsweise Alter, PS, Farbe, etc. ermittelt werden. In den Screenshots finden Sie zu den Orange markierten Bereichen einige nützliche Erläuterungen.

Tab 1: Überblick Regressionsszenario

Die nachfolgende Abbildung bietet Ihnen einen Gesamtüberblick auf das Ergebnis der Prognose und die der Prognose zu Grunde liegenden Settings.

Analyse des Beitrags einzelner Einflussfaktoren

In diesem Tab finden sie nützliche Informationen zu den Haupteinflussfaktoren und deren Einfluss auf das Ergebnis.

Szenario 3: Klassifikation (Classification)

Bei der Klassifikation (Classification) geht es darum, die Wahrscheinlichkeit eines zukünftigen Ereignisses abzuschätzen. In der Trainingsphase wird das Modell mit Vergangenheitsdaten gefüttert in denen beobachtet wurde, ob das Ereignis auf einer bestimmten Granularität (Ebene) für die Key Variable wie Kunde, Mitarbeiter, Produkt beobachtet wurde oder nicht. Auf Basis dieser Trainingsdaten kann das System ein Vorhersagemodell erstellen, mit dem die Wahrscheinlichkeit des Eintreffens eines Ereignisses für einen neuen Anwendungsdatensatz vorhergesagt werden kann.

Folgende Fragestellungen können dabei beispielsweise betrachtet werden:

Wird ein Mitarbeiter das Unternehmen verlassen oder nicht? Werden einzelne Kunden positiv oder negativ auf eine Werbekampagne reagieren? Wird eine Maschine in der Fertigung bald ausfallen oder nicht? Handelt es sich bei einer E-Mail um Spam oder nicht?

Wie Sie sehen können, handelt es bei den Ereignissen um binäre Events mit zwei möglichen Ergebnissen: Mitarbeiter verlässt das Unternehmen oder Mitarbeiter bleibt im Unternehmen, Kunde reagiert positiv auf eine Werbekampagne oder Kunde reagiert negativ die Kampagne, Maschine fällt aus oder Maschine fällt nicht aus, etc.

Um diese Entscheidung fällen zu können, ermittelt das System eine Funktion, mit der die Wahrscheinlichkeit des Eintretens des Ereignisses als Wert zwischen 0 % und 100 % kalkuliert wird. Zusammen mit einem vorher festgelegten Schwellwert von beispielsweise 50 % kann das System den Ergebniswert einem der beiden möglichen Ereignisergebnisse zuweisen. Ist beispielsweise die Wahrscheinlichkeit, dass ein Kunde positiv auf eine Marketingkampagne reagiert, 60 %, so klassifiziert das System diesen Kunden als „reagiert positiv auf die Marketingkampagne“ und schreibt einen entsprechenden Wert in die Zielvariable.

Viele der Techniken, mit der das System das Ergebnis der Kategorisierung prognostiziert, sind die gleichen wie bei der Regression. Auch bei der Kategorisierung nutzt das System die Technik der Entscheidungsbäume, um der Komplexität der gesuchten Wahrscheinlichkeitsunktion mit einer unter Umständen hohen Anzahl von Einflussvariablen und Ausprägungen Herr zu werden. Die Einflussvariablen können sowohl Dimensionen (nominale Variablen wie das Geschlecht eines potenziellen Kunden) als auch Kennzahlen (numerische Werte wie das bisherige Einkaufsvolumen eines Kunden) sein.

Das Ergebnis eines Zweiges des Entscheidungsbaumes ist im Gegensatz zur Regression aber nicht ein absoluter Wert, sondern eine prozentuale Wahrscheinlichkeit. Um diese Transformation zu erreichen, wird auf alle Ergebnisse des Entscheidungsbaumes die sogenannte Sigmoid Funktion angewandt.

Diese invertierbare Funktion ordnet allen ermittelten Kennzahlenwerten des Entscheidungsbaums einen Wert zw. 0 und 1 beziehungsweise zwischen 0 und 100 % zu. Wie auch bei der Regression kommt dabei nicht „Der Eine Entscheidungsbaum“ zum Einsatz. Vielmehr wird, wie auch beim Regressionsverfahren, das sogenannte Gradient Boosting eingesetzt, in dem mehrere Entscheidungsbäume aufgebaut und bei der Ergebnisfindung kombiniert werden. Dieses sorgt auch bei der Klassifikation dafür, dass es nicht zum Over- oder Underfitting und stattdessen zu einem „gesunden“ Gleichgewicht zwischen der Tiefe bzw. Komplexität des Entscheidungsbaums (Anzahl von Verzweigungen) und des für den Baum berechneten Fehlermaßes Total Loss kommt. In der Abfolge wird das nächste Modell so aufgebaut, dass das Ergebnis der Verlustfunktion des Entscheidungsbaumensembles weiter minimiert wird. Die Verlustfunktion misst für alle Beobachtungspunkte die Differenz zwischen der Vorhersage des Modells und dem tatsächlichen Wert. 

Beispiel eines Klassifikationsszenarios in der SAC

Schauen wir uns in den nachfolgenden Screens ein typisches Klassifikationsszenario in der SAC an. Darin soll ermittelt werden, ob für einzelne Mitarbeiter ein erhöhtes Risiko besteht, dass sie die Firma verlassen (sogenanntes Flight Risk).

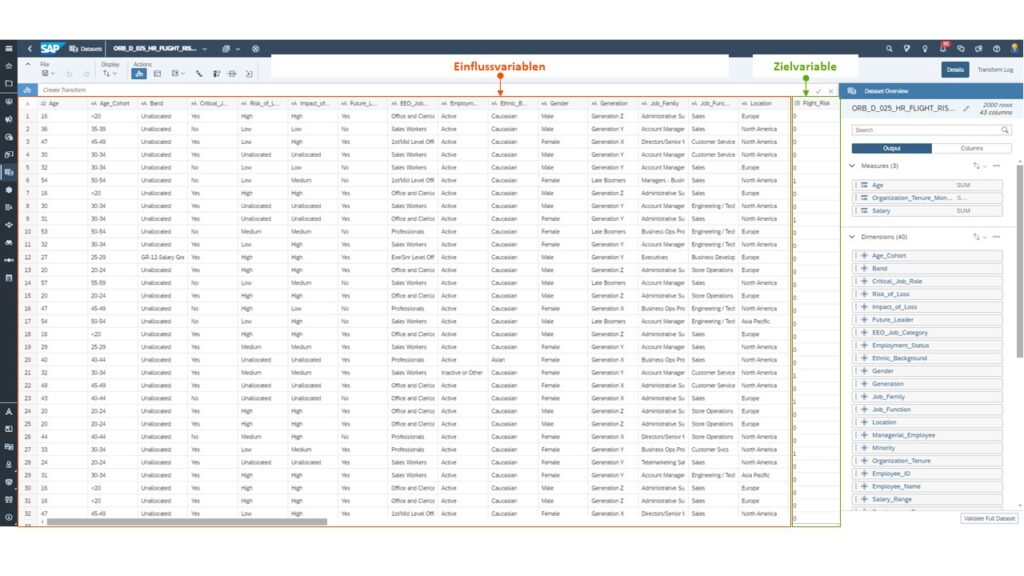
Trainingsdatenset

Anbei ein Überblick über ein Trainingsdatenset mit den Einflussvariablen (Age, Gender, etc.) und der Zielvariable (Flight Risk)

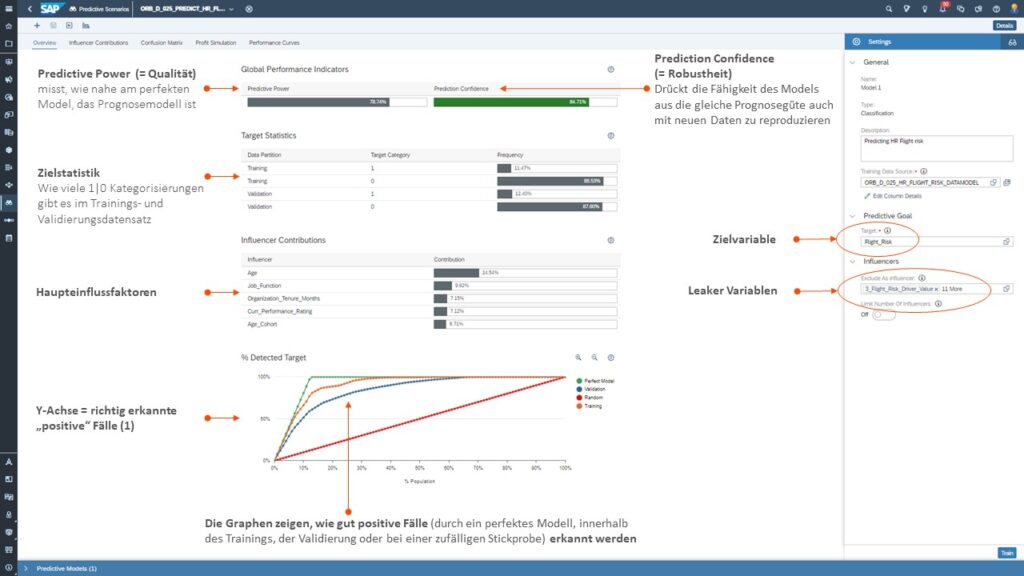
Tab 1: Überblick zur Klassifikation und deren Aussagekraft

Die nächste Abbildung zeigt die Setting Einstellungen des Modells und gibt Ihnen anhand von bestimmten Messgrößen Auskunft darüber, wie gut das Modell ist.

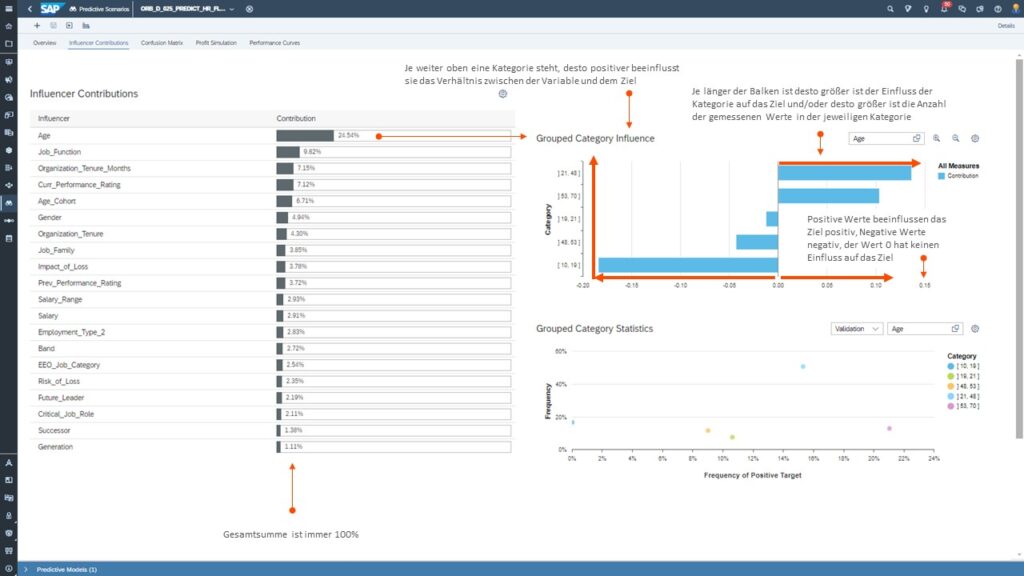
Tab 2: Einflussfaktoren in der Klassifikation

Nachfolgend ein Ausschnitt, der zeigt was die Haupteinflussfaktoren sind und welche Kategorien (z.B. {10, 19}, {48, 53}, usw.) das System für die Faktoren jeweils ermittelt hat:

Tab 3: Fehlermatrix (Confusion matrix)

Die Konfusionsmatrix (auch als Wahrheitsmatrix, Fehlermatrix oder engl. Confusion Matrix bekannt) ist ein spezielles Werkzeug, das in der maschinellen Lernwelt (engl. Machine Learning) verbreitet ist. Sie kann die Qualität eines Klassifikationsmodells im Machine Learning beurteilen. Hierbei zeigt sie, wie viele der Vorhersagen richtiger- oder fälschlicherweise einer Klasse zugeordnet wurden. Genaue Erläuterungen zu unserem Beispiel hinsichtlich der Simulation von Kontaktszenarien und den damit verbundenen Metriken finden Sie im Screenshot unterhalb:

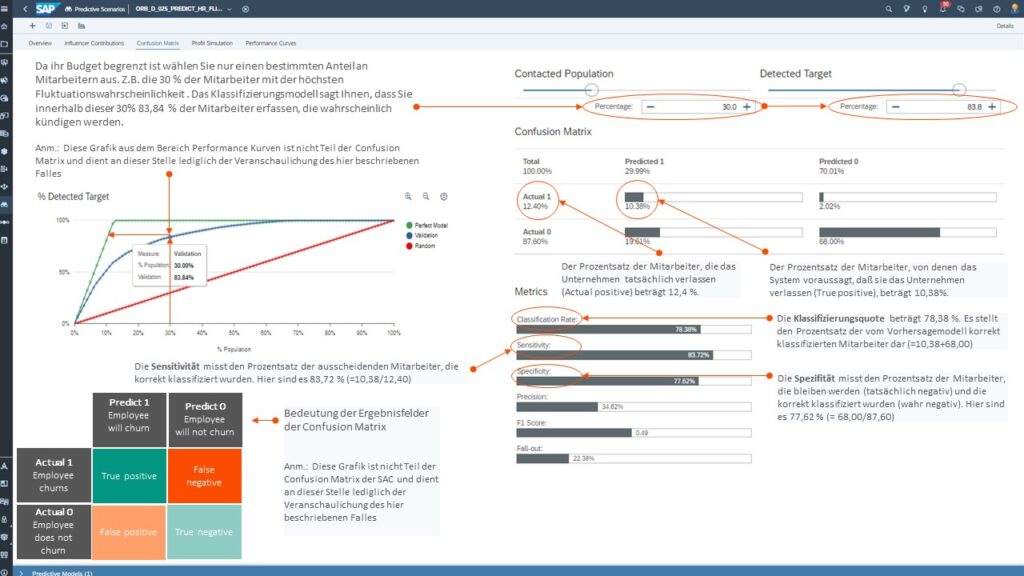
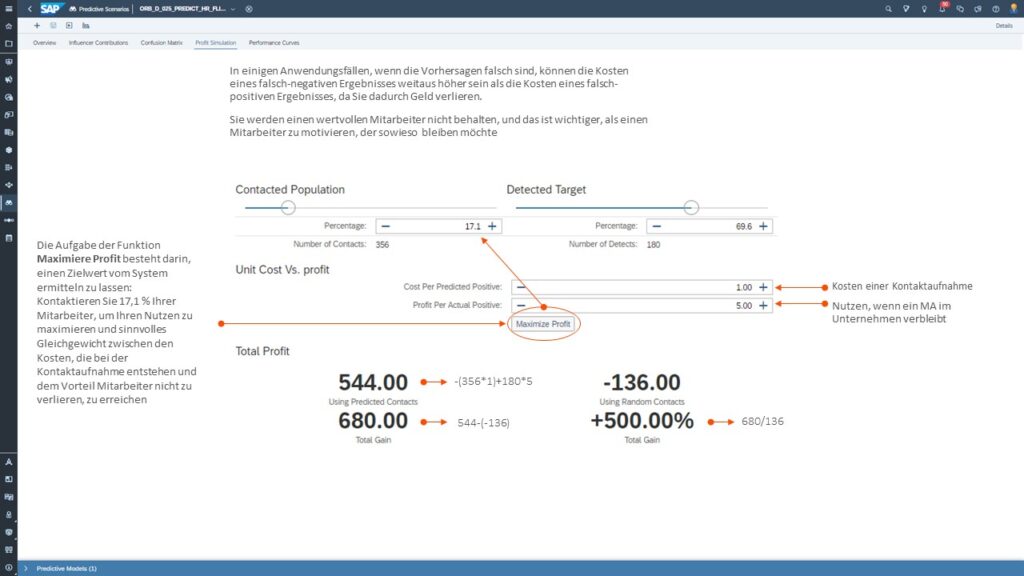
Tab 4: Gewinnsimulation (Profit Simulation)

Mittels der Gewinnsimulation ist nun eine Maximierung des Nutzens durch Findung des besten Kontaktszenarios möglich:

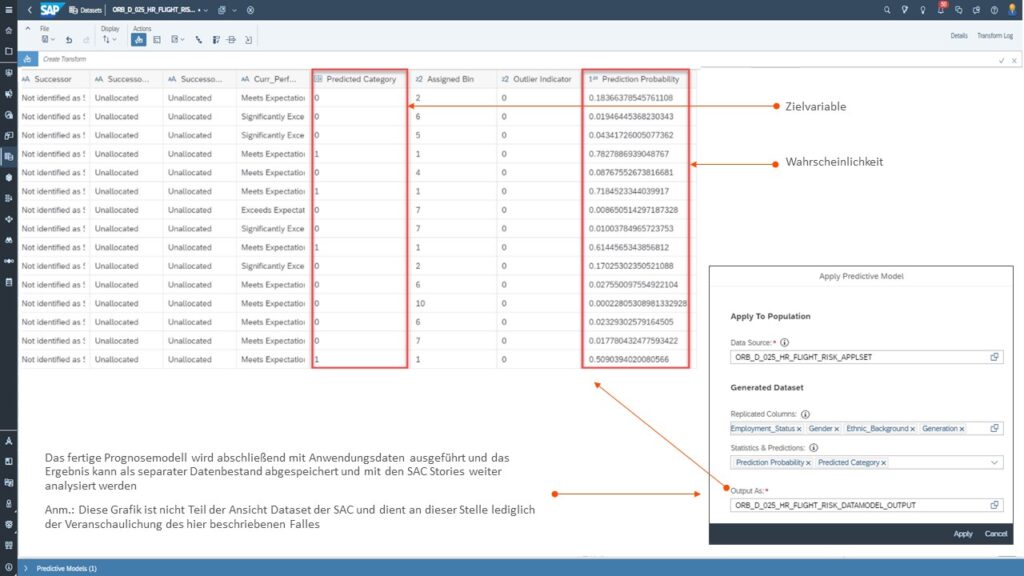
Ergebnis der Klassifikation

Das fertige Prognosemodell kann abschließend mit den eigentlichen Anwendungsdaten ausgeführt werden. Das Ergebnis kann als separater Datenbestand abgespeichert und mit den SAC Stories weiter analysiert werden:

Zusammenfassung und Vorteile von Augmented Analytics auf einen Blick

Neben dem Just Ask Chatbot (Vorteil 1), dem digitalen Assistenten, mit dem Sie in natürlicher Sprache kommunizieren können, bietet Augmented Analytics auch Prognosemöglichkeiten (Predictive Analytics, Vorteil 2). Diese bilden einen großen Mehrwert durch die Smart Predict ML-Algorithmen.

Ein weiterer Vorteil sind die schnelle Datenanalyse und die präzisen Ergebnisse (Vorteil 3), sodass Sie große Datenmengen in kürzester Zeit analysieren und verwertbare Erkenntnisse gewinnen können.

In der umfassenden, cloudbasierten SAC-Plattform unterstützen KI-Funktionen sowohl die dort implementierten Planungs- als auch Reportingprozesse (Vorteil 4). Ein weiterer Vorteil dieser Lösung ist, dass die KI-Funktionen ohne zusätzliche Kosten direkt genutzt werden können (Vorteil 5).

Und nun, nachdem Sie die Prognoseszenarien mit Smart Predict und deren Funktionsweise entdeckt haben? It‘s your turn!

Die Einbettung von KI in die SAC bietet ein enormes Potenzial für Ihr Unternehmen. Für Sie als Anwender besteht der große Nutzen vor allem darin, dass Sie die Mechanismen derer sich die KI bedient, nur rudimentär in seinen Grundprinzipien, nicht aber in ihrer ganzen technischen und mathematischen Tiefe verstehen müssen. Diese Aufgabe kann im Regelfall getrost den Technikern und Data-Scientists der SAP oder anderen Anbietern überlassen werden, die diese vorgedachten Grundfunktionen in ihre Produkte implementiert haben. Sie müssen im ersten Schritt lediglich die konkreten Fragestellungen und Usecases in Ihrem Unternehmen identifizieren, bei deren Lösung bzw. Bearbeitung Ihnen die oben beschriebenen Augmented Analytics Funktionen helfen können.

Als Anwender sollten Sie jedoch ein tiefes, ganzheitliches Verständnis für Ihre Daten besitzen. Nur so können Sie der KI die richtigen Fragen stellen und die Rahmenparameter für die Verarbeitung durch das System richtig setzen.  Zusätzlich ist es Ihre Aufgabe, die Unternehmensdaten, die von der KI verwendet werden, sicher zu speichern, qualitativ hochwertig aufzubereiten und in einer gut strukturierten Form auf semantischer Ebene bereitzustellen. Stichwort Data Governance.

Pssst… Hier ein wertvoller Praxistipp für Sie

Achten Sie darauf, dass Sie mit vielen Datensätzen arbeiten, nur so kann das System ein robustes Modell erstellen. Experimentieren Sie mit unterschiedlichen Modellparametern und -konfigurationen, um das beste Ergebnis zu erhalten. Finden Sie die richtigen Variablen (beeinflussende Dimensionen und Kennzahlen) im Datensatz. Identifizieren Sie die sogenannten Leaker-Variablen und exkludieren Sie diese in der Trainingsphase. Leaker-Variablen sind Variablen, die unbeabsichtigt Informationen über die Zielvariable enthalten und dadurch die Vorhersage verfälschen können.

Möchten Sie langfristig erfolgreich sein? Dann ist es wichtig, die strategische Bedeutung von Cloud-Computing, künstlicher Intelligenz und maschinellem Lernen zu erkennen und die gebotenen technologischen Fortschritte zu nutzen. Wir unterstützen Sie gerne in diesem Prozess.

P.S.: Ein besonderer Dank geht an dieser Stelle an meinen geschätzten Kollegen Mirko Fuchs für die interessanten Diskussionen zum Thema KI und fürs Korrekturlesen dieses Blogs.